Нормальная форма Чибрарио

Нормальная форма Чибрарио — нормальная форма дифференциального уравнения, не разрешённого относительно производной, в окрестности простейшей особой точки. Название предложено В. И. Арнольдом в честь итальянского математика Марии Чибрарио, установившей эту нормальную форму для одного класса уравнений.

Связанные определения

Особые точки

Пусть дифференциальное уравнение имеет вид

[math]\displaystyle{ F(x,y,p) = 0, \ }[/math] где [math]\displaystyle{ p=\frac{dy}{dx}. }[/math]

Функция [math]\displaystyle{ F }[/math] предполагается вещественной, гладкой класса [math]\displaystyle{ C^{\infty} }[/math] (или аналитической) по совокупности всех трёх переменных. Особые точки такого уравнения — это точки трёхмерного пространства с координатами [math]\displaystyle{ (x,y,p) }[/math], лежащие на поверхности, задаваемой уравнением [math]\displaystyle{ F=0 }[/math], в которых производная [math]\displaystyle{ F_p }[/math] обращается в нуль, т. е. проектирование [math]\displaystyle{ \pi }[/math] поверхности [math]\displaystyle{ \{F=0\} }[/math] на плоскость переменных [math]\displaystyle{ x,y }[/math] вдоль направления оси [math]\displaystyle{ p }[/math] нерегулярно. В общем случае множество особых точек образует на поверхности [math]\displaystyle{ \{F=0\} }[/math] кривую, называемую криминантой. Проекция криминанты на плоскость [math]\displaystyle{ (x,y) }[/math] называется дискриминантной кривой, её точки тоже часто называют особыми точками уравнения, хотя при этом возможна неточность: при проектировании [math]\displaystyle{ \pi }[/math] различным точками поверхности [math]\displaystyle{ \{F=0\} }[/math] может соответствовать одна и та же точка плоскости переменных [math]\displaystyle{ (x,y) }[/math].

Поднятие уравнения

Дифференциальное соотношение [math]\displaystyle{ p=dy/dx }[/math] задает в пространстве [math]\displaystyle{ (x,y,p) }[/math] поле контактных плоскостей [math]\displaystyle{ pdx-dy=0 }[/math]. Пересечение контактных плоскостей с плоскостями, касательными к поверхности [math]\displaystyle{ \{F=0\} }[/math], задает на последней поле направлений (определенное во всех точках, где контактные и касательные плоскости не совпадают друг с другом). Интегральные кривые построенного таким образом поля являются 1-графиками решений исходного уравнения, а их проекции на плоскость [math]\displaystyle{ (x,y) }[/math] — графиками решений

Поднятие уравнения на поверхность

Описанная конструкция исследования уравнений, не разрешённых относительно производной, восходит к третьему мемуару А. Пуанкаре «О кривых, определяемых дифференциальными уравнениями» (1885); в современной математической литературе она часто называется поднятием уравнения на поверхность.

Теорема о нормальной форме

Простейшими особыми точками уравнения [math]\displaystyle{ F(x,y,p)=0 }[/math] являются так называемые регулярные особые точки, в которых проектирование [math]\displaystyle{ \pi }[/math] имеет особенность, называемую складкой Уитни, и контактная плоскость не касается поверхности [math]\displaystyle{ F=0. }[/math] Это равносильно выполнению в данной точке условий:

[math]\displaystyle{ F=0, \quad F_p=0, \quad F_{pp} \neq 0, \quad F_x + pF_y \neq 0. }[/math]

Теорема. В окрестности регулярной особой точки уравнение [math]\displaystyle{ F(x,y,p)=0 }[/math] с гладкой (или аналитической) функцией [math]\displaystyle{ F }[/math] гладко (соответственно, аналитически) эквивалентно уравнению [math]\displaystyle{ p^2-x = 0, }[/math] называемому нормальной формой Чибрарио.

В 1932 году Чибрарио получила эту нормальную форму, исследуя характеристики уравнения с частными производными второго порядка смешанного типа.

Примеры

Нормальная форма Чибрарио является характеристическим уравнением для уравнения Трикоми

[math]\displaystyle{ u_{xx}-x u_{yy} = 0 }[/math],

относящегося к эллиптическому типу в полуплоскости [math]\displaystyle{ x\lt 0 }[/math] и к гиперболическому — в полуплоскости [math]\displaystyle{ x\gt 0 }[/math].

Семейство решений в нормальной форме Чибрарио

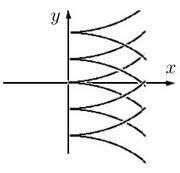
Уравнение [math]\displaystyle{ p^2-x=0 }[/math] легко интегрируется: графики его решений образуют семейство полукубических парабол

[math]\displaystyle{ y= \pm \frac{2}{3} x^{\frac{3}{2}} + \rm const, }[/math]

заполняющих полуплоскость [math]\displaystyle{ x\gt 0 }[/math], точки возврата которых лежат на дискриминантной кривой — оси [math]\displaystyle{ y }[/math].

Аналогичным образом выглядят асимптотические линии двумерной поверхности в евклидовом пространстве в окрестности типичной параболической точки. Нормальная форма Чибрарио соответствует также простейшим особенностям поля медленного движения в быстро-медленных динамических системах.

Литература

• Арнольд В. И. Дополнительные главы теории обыкновенных дифференциальных уравнений, — Любое издание.
• Арнольд В. И. Геометрические методы в теории обыкновенных дифференциальных уравнений, — Любое издание.
• Арнольд В. И., Ильяшенко Ю. С. Обыкновенные дифференциальные уравнения, — Итоги науки и техн. Сер. Совр. пробл. мат. Фундам. направ., 1985, том 1.
• Арнольд В. И., Афраймович В. С., Ильяшенко Ю. С., Шильников Л. П. Теория бифуркаций, — Итоги науки и техн. Сер. Совр. пробл. мат. Фундам. направ., 1986, том 5.
• Cibrario M. Sulla reduzione a forma canonica delle equazioni lineari alle derivative parzialy di secondo ordine di tipo misto, — Rend. Lombardo 65 (1932), pp. 889–906.